The limit of a function is said to be a value, which gets closer to the variable that approaches some number. Usually, the limits of a function are used for defining the integrals, derivatives, and continuity by determining the limit of the given number. Sometimes the calculation of the limit becomes daunting and complex.
The calculation is also time-consuming when you don’t follow the rules of its calculations. To make things a bit easier, you can try the online limit calculator, through which you can calculate the positive and negative limits for a given function at any point.
In this guidepost, you will know about how to calculate the functions limit algebraically.
How to Define the Limit of a Function?
Suppose “f” is a function and “b” is the continuous quantity, a real number. The equation of limit according to the limit formula would be written as follows:
bf(x) =L
his will show you that the function f(x) can be considered to be equal to “L” by making x closer to the b. so, you can say that the expression mentioned above is defined as the limit of the function(x) by considering this case. Here x is approaching be and is equal to L.
This calculation for limits gets complicated sometimes, but nothing to worry about. Use the find the limit calculator with steps that show each limit calculation step in the blink of an eye. This limit evaluation calculator is the best tool to determine the limit because it uses the limit calculation standard formula.
How to Solve Limit Function Manually?
For the calculation of limits of a functions, let’s suppose that x=1
= x2 – 1/ x – 1
= 12 -1 / 1 – 1
= 0/0
As you know this is indeterminate or undefined, so we use another way for the calculation limit of a function. Instead of using x = 1, we need to try to approach it a bit closer to it mentioned below table:
| X | (x2 − 1)/(x − 1) |
| 0.25 | 1.0625 |
| 0.45 | 1.2025 |
| 0.9 | 1.810 |
| 0.99 | 1.99000 |
Now, we know that the variable x gets closer to 1, and the other function is closer to 2. So, it can be described as:
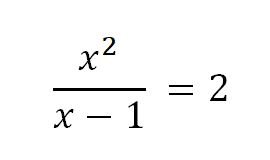
How does Limit Calculator determine Limits?
They find the limit calculator finds the interval nearby x for any chosen nearest degree. This is because, the provided value of function f(x) varies from L by the quantity less than ε (i.e., if ε= |x − x0| < δ as compared to the |f (x) − L| < ε).
Below is the procedure to determine the limits by using the limits calculator.
The first step of calculating limits is to put the equation or function you want to calculate. Now, select the variable by using the drop-down menu with respect to which you are required to calculate the limit. It might be a, b, c, x, y,z, or n. After the variable selection, you are required to specify the number at which you want to determine the limit.
In this section, you can use simple expressions like inf=∞ or pi =π. After that, you need to make the limit direction that can be negative or positive. Once you enter the values, then hit the calculate button.
When you hit the calculate button, the online find the limit calculator will process the values to show you the step-by-step procedure of calculation with the representation of Taylor’s series expansion for the function you are calculating. This calculator shows the easy steps that will teach how to find limits.
Conclusion
In this article, the main focus of the topic is to discuss how to find the limit. This post shows the manual procedure for limit calculation and finds the limit calculator calculation. The manual procedure becomes easier when you follow all the instructions, but the most suitable approach is using the limit equation calculator.




